Zad. 1. Jaką największą wartość może przyjąć najmniejsza z liczb dodatnich: x, y + 1/x, 1/y?
Zad. 2. Rozwiąż równanie [n/2]–[n/3] = 50 w zbiorze liczb naturalnych. Symbol [a] oznacza część całkowitą liczby a.
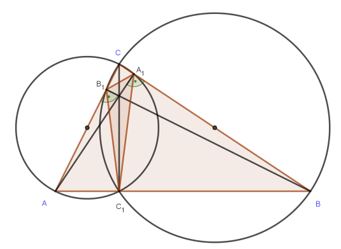
Zad. 3. Wykaż, że punkt przecięcia wysokości trójkąta ostrokątnego jest środkiem okręgu wpisanego w trójkąt spodkowy (tzn. taki, którego wierzchołki są spodkami wysokości wyjściowego trójkąta).
W czerwcu punkty zdobyli:
• 3 pkt. – Joanna Lisiowska XXI LO Warszawa i Jakub Dobrzański LO I Lubin;
• 2 pkt. – Bartłomiej Zug LO Oleśno;
• 0,5 – Mikołaj Dyblik LO 7 Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Oznaczmy przez s największą wartość, jaką przyjmuje najmniejsza z liczb x, y+1/x, 1/y dla pewnych wartości x, y ∈ R+. Wówczas x ≥ s (lub równoważnie 1/x ≤ 1/s), y+1/x ≥ s oraz 1/y ≥ s (lub równoważnie y ≤ 1/s). Stąd otrzymujemy nierówność podwójną s ≤ y+1/x ≤ 2/s (bo y ≤ 1/s oraz 1/x ≤ 1/s), z której wynika (dla s ∈ R+), że s2 ≤ 2, czyli s ≤ √2. I ta wartość jest przez s osiągana, np. dla x=√2 i y = √2/2.
Zad. 2. Weźmy funkcję f okeśloną na liczbach naturalnych f(n) = [n/2] – [n/3]. Szukamy takich n, dla których f(n) = 50. Rozważmy przypadki, ze względu na resztę z dzielenia n przez 6. Dla pewnego k naturalnego zachodzi:
a) n = 6k, f(n) = f(6k) = [3k]–[2k] = 3k–2k = k, zatem k=50 i n=300.
b) n = 6k+1, f(n) = f(6k+1) = [3k+1/2]–[2k+1/3] = 3k–2k = k, zatem k=50 i n=301.
c) n = 6k+2, f(n) = f(6k+2) = [3k+1]–[2k+2/3] = 3k+1 – 2k = k+1, zatem k=49 i n=296.
d) n = 6k+3, f(n) = f(6k+3) = [3k+1+1/2]–[2k+1] = 3k+1 – (2k+1) = k, zatem k=50 i n=303.
e) n = 6k+4, f(n) = f(6k+4) = [3k+2]–[2k+1+1/3] = 3k+2 – (2k+1) = k+1, zatem k=49 i n=298.
f) n = 6k+5, f(n) = f(6k+5) = [3k+2+1/2]–[2k+1+2/3] = 3k+2 – (2k+1) = k+1, zatem k=49 i n=299.
Wobec tego rozwiązaniem równania jest zbiór {296, 298, 299, 300, 301, 302}.
Zad. 3. Niech AA1, BB1, CC1 będą wysokościami trójkąta ABC. Opiszmy okręgi na trójkątach ACC1 i BCC1. Kąty B1C1C i B1BC są równe (wpisane, oparte na tym samym łuku). Analogicznie równe są kąty CC1A1 i CAA1. Ale trójkąty CAA1 i CBB1 są podobne (cecha kąt-kąt), więc
kąty CAA1 i CBB1 są równe, co z przechodniości daję równość kątów B1C1C i CC1A1, a to oznacza, że wysokość CC1 jest dwusieczną kąta B1C1A1. To samo rozumowanie prowadzimy dla pozostałych kątów. Stąd punkt przecięcia wysokości trójkąta ABC jest punktem przecięcia dwusiecznych kątów trójkąta A1B1C1, a co za tym idzie - środkiem okręgu wpisanego w ten trójkąt.
