| więcej informacji o tekście: |
Definicja:
Romb to czworokąt płaski równoboczny (tzn. ma wszystkie boki przystające).
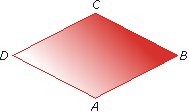
Oznaczenie:
$\diamond$ABCD (czytaj: romb o wierzchołkach A, B, C, D)
Pochodzenie nazwy:
Nazwa romb pochodzi od greckiego rhómbos, co oznacza czworobok o wszystkich bokach równej długości.
Elementy składowe rombu:
- punkty A, B, C i D to wierzchołki rombu
- odcinki AB, BC, CD i DA to boki rombu
- odcinki AC i BD to przekątne rombu
- odległość między przeciwległymi bokami to wysokość rombu
- łamana zamknięta ABCDA to brzeg rombu
Konstrukcja:
Definicje alternatywne:
- równoległobok o równych sąsiednich bokach
- równoległobok o prostopadłych przekątnych
- równoległobok z osią symetrii
- równoległobok, którego przekątna połowi kąt wewnętrzny
- równoległobok, w który można wpisać okrąg
Przykłady:
- kwadrat (rys. 1)
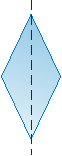
- kształt 'karo' (romb o kącie wewnętrznym 45°) (rys. 2)
- 'kopnięty kwadrat' (rys. 3)
- dwa przystające trójkąty równoramienne sklejone podstawami (rys. 4)
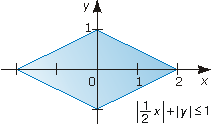
- romb opisany na okręgu i wpisany w elipsę (rys. 5)
- romb w układzie współrzędnych zadany nierównością $|\frac{1}{2}x|+|y|\leq1$ (rys. 6)
 |  |  |   |
| Rys. 1 | Rys. 2 | Rys. 3 | Rys. 4 |
 |  |
| Rys. 5 | Rys. 6 |
Kontrprzykłady:
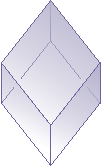
- romboid (lub deltoid) - nieprzystające trójkąty równoramienne sklejone podstawami (rys. 1)
- romboedr (lub rombościan) - nie jest wielokątem (rys. 2)
- superelipsa zadana w układzie współrzędnych nierównością $|\frac{1}{2}x|^{\frac{2}{3}}+|y|^{\frac{2}{3}}\leq1$ - nie jest wielokątem (rys. 3)
 |  |  |
| Rys. 1 | Rys. 2 | Rys. 3 |
Własności:
- przekątne rombu są prostopadłe
- romb ma dwie osie symetrii (przekątne)
- romb ma środek symetrii (punkt przecięcia przekątnych)
- w każdy romb można wpisać okrąg
- środkiem okręgu wpisanego w romb jest punkt przecięcia przekątnych
- na każdym rombie można opisać elipsę
- romby szczelnie wypełniają płaszczyznę (tworzą parkietaż)
- cecha przystawania rombów - (bk)
- cecha podobieństwa rombów - (k)
- romb o przystających kątach wewnętrznych to kwadrat
Związki miarowe:
W rombie o boku długości a, jednym z kątów wewnętrznych o mierze $\alpha$ i przekątnych długości d1 i d2 mamy:
- wysokość h = a sin$ \alpha$
- pole P = ah = $\frac{1}{2}$d1d2 = a2 sin $\alpha$
- obwód O = 4a
- przekątne d1 = $2a\sin{\frac{\alpha}{2}}$, d2 = $2a\cos{\frac{\alpha}{2}}$
- drugi kąt wewnętrzny wynosi 180°-$\alpha$
- suma kątów wewnętrznych wynosi 360°
- suma kątów zewnętrznych wynosi 360°
- promień okręgu wpisanego r = $\frac{1}{2}h$ = $\frac{1}{2}a\sin{\alpha}$
Historia:
- Romb był popularnym motywem w starożytnym zdobnictwie.
 |  |  |  |
| Fot. 1 | Fot. 2 | Fot. 3 | Fot. 4 |
Fot. 1. Fragment kości konia z 11 tysiąclecia p.n.e. z okolic Cuina Turcului w Rumunii.
Fot. 2. Figura z Gladnioe w Jugosławii z ok. 6000 r. p.n.e.
Fot. 3. Gliniana figura z okolic Rast w Rumunii z ok. 5200 r. p.n.e.
Fot. 4. Lady of Pazardjic z Bułgarii z ok. 4500 r. p.n.e.
- Euklides w IV w. p.n.e. w swoim dziele Elementy opisuje romb jako tę z figur czworobocznych, która jest równoboczna, ale nie prostokątna.
- Irański matematyk Al-Kaszi w dziele Klucz arytmetyki z 1427 roku w części dotyczącej czworokątów wyróżnia romby jako te o równych bokach i nierównych kątach.
Terminy pokrewne:
- złoty romb
Bibliografia:
- Encyklopedia szkolna. Matematyka, WSiP, Warszawa 1997
- W. Więsław, Matematyka i jej historia, Nowik, Opole, 1997
- Euklides, Elementy, http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
- J. Zydler, Geometria, http://www.wiw.pl/matematyka/geometria
- http://library.thinkquest.org/C006353/from_rhombus_to_internet.html
- http://mathworld.wolfram.com




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
