Dolnośląski Ośrodek Doskonalenia Nauczycieli
ul. Trzebnicka 42-44
50-230 Wrocław
https://dodn.dolnyslask.pl
Partnerzy:
Uniwersytet Ekonomiczny we Wrocławiu
Uniwersytet Wrocławski we Wrocławiu
Wyższa Szkoła Zarządzania i Przedsiębiorczości w Wałbrzychu
Collegium Witelona Uczelnia Państwowa
Fundacja Pro Mathematica we Wrocławiu
Zespół Szkół Ekonomiczno-Administracyjnych we Wrocławiu
Zespół Szkół Nr 7 w Wałbrzychu
Zespół Szkół Ekonomicznych w Legnicy
Zespół Szkół Ekonomiczno-Turystycznych w Jeleniej Górze
Honorowy patronat:
Rektor Uniwersytetu Ekonomicznego
Rektor Uniwerytetu Wrocławskiego
Rektor Wyższej Szkoły Zarządzania i Przedsiębiorczości w Wałbrzychu
Rektor Collegium Witelona Uczelnia Państwowa
Dolnośląski Kurator Oświaty
zgłoszenia do 15 stycznia 2025 online
I etap - 20 lutego 2025
II etap - 12 marca 2025
III etap – 9 kwietnia 2025
uroczyste zakończenie - 22 maja 2025
Konkurs promuje edukację ekonomiczną wśród uczniów starszych klas szkół podstawowych, uczy przedsiębiorczości i podejmowania decyzji dotyczących m.in. lokat, kredytów i buchalterii domowej. Patronat honorowy nad konkursem objął Rektor Uniwersytetu Ekonomicznego. Od roku szkolnego 2012/13 rozgrywany jest podobny konkurs dla uczniów klas 4-6 szkół podstawowych.
Pierwsza edycja konkursu odbyła się w roku szkolnym 2006/2007. Organizatorem było wówczas Wrocławskie Centrum Doskonalenia Nauczycieli. Konkurs adresowany był do gimnazjalistów i cieszył się sporym zainteresowaniem. W latach 2009-2017 roku konkurs organizowany był we współpracy z Wyższą Szkołą Handlową we Wrocławiu, a w roku szkolnym 2017/2018 - we współpracy z Wyższą Szkołą Bankową we Wrocławiu. Począwszy od drugiej edycji konkurs dofinansowany jest ze środków Narodowego Banku Polskiego w ramach programu edukacji ekonomicznej. Od roku szkolnego 2019/2020 organizatorem konkursu jest Dolnośląski Ośrodek Doskonalenia Nauczycieli we współpracy z Uniwersytetem Ekonomicznym.
- Konkurs skierowany jest do uczniów klas 7-8 szkół podstawowych województwa dolnośląskiego.
- Etap szkolny. W tym etapie szkoły wyłaniają 3-osobowe zespoły, które reprezentują je w II etapie zawodów. Uczniowie pracują indywidualnie, rozwiązując testy wielokrotnego wyboru (40 zadań na 60 minut).
- Etap I. Uczniowie pracują indywidualnie, rozwiązując testy wielokrotnego wyboru, testy uzupełnienia i testy krótkiej odpowiedzi (40 zadań na 60 minut). Wynik drużyny to suma punktów uzyskanych przez jej członków. Do III etapu jest kwalifikowanych 10 najlepszych drużyn. W przypadku remisów przeprowadza się dogrywkę.
- Etap II. Składa się z trzech rund po 30 minut. Uczniowie pracują zespołowo, rozwiązując zadania otwarte, krzyżówki, rebusy, inscenizując scenki itp. Laureatami zostają trzy najlepsze drużyny. W razie remisu odbywa się dogrywka.
Etap I
1. Bank pobiera za usługę opłatę (zwaną prowizją) wynoszącą 0,5% wpłacanej kwoty, lecz nie mniej niż 4,50 zł. Za rachunek telefoniczny na kwotę 800 zł prowizja wynosi:
A. 4 zł B. 4,50 zł C. 8 zł D. 40 zł
2. Pan Wiśniewski postanowił kupić małe mieszkanie. W gazecie znalazł 4 oferty. Które z tych mieszkań jest najtańsze?
A. Mieszkanie jednopokojowe, 35 m2, jasna kuchnia, 2300 zł/m2 .
B. OKAZJA! Słoneczne, małe (36 m2) mieszkanie za jedyne 82 tys. zł.
C. Mieszkanie o powierzchni 32 m2, cena 2100 zł/m2 + 22% VAT.
D. Mieszkanie willowe 150 m2, jedynie 1800 zł/m2.
3. Księgarz obniżył o 10% planowaną początkowo cenę atlasu, a mimo to jego zysk wyniósł 8%. Jaki był planowany początkowo zysk ze sprzedaży tego atlasu?
A.30% B. 12% C. 18% D. 20%
Etap II
Firma telekomunikacyjna TELEGADUŚ oferuje trzy rodzaje taryf.
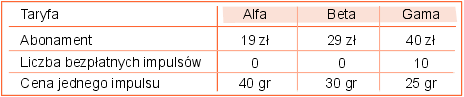
1. Dla osób wykorzystujących miesięcznie mniej niż 100 impulsów najkorzystniejsza jest taryfa:
A. Alfa B. Beta C. Alfa i Beta D. Gamma
2. Przy jakiej liczbie impulsów najkorzystniejsza jest taryfa Gamma?
3. Spośród skrótów: BID, BIN, NIP, NRB, PIN, PIT, SDR, SPA wybierz trzy i dopasuj do definicji.
a) Jednoznaczny identyfikator rachunku bankowego. W polskim systemie numeracji rachunków składa się z 26 cyfr.
b) Pierwsze 6 cyfr w numerze karty płatniczej, pozwalają one na zidentyfikowanie banku - emitenta oraz organizacji płatniczej, która wydała kartę.
c) Osobisty numer identyfikujący posiadacza karty, zastępuje jego podpis i jest niezbędny do przeprowadzania wszelkich transakcji z użyciem karty. W Polsce numer ten składa się najczęściej z 4 cyfr.
Etap III
1. Puszki z groszkiem sprzedaje się w supermarkecie po 1,60 zł. Tygodniowo sprzedaje się 400 puszek. Kierownik szacuje, że każde 10 gr obniżki spowodowałyby dodatkową sprzedaż 100 puszek tygodniowo. Supermarket kupuje puszki od producenta płacąc 1 zł za puszkę. Jaką cenę powinien ustalić sprzedawca, aby jego zysk był największy?
Zapisz wzór zależności zysku od wartości obniżki ceny puszki groszku.
2. W 2000 roku Ewa - mieszkanka Warszawy - była na wakacjach w Grecji. Noclegi i przelot opłaciła w biurze podróży. Potrzebowała jeszcze kupić drachmy na wyżywienie i inne wydatki. Na zakup waluty Ewa przeznaczyła 1720 zł. W pobliskim kantorze Wisła drachm akurat nie było. Ewa postanowiła kupić marki albo dolary i wymienić je w Grecji w kantorze Adonis. Co powinna kupić, aby wymiana była dla niej korzystniejsza?
3. Wpłaciłeś 100 zł na konto, którego oprocentowanie jest równe 10% w stosunku rocznym. Jaka będzie realna wartość twoich pieniędzy po roku, jeżeli inflacja roczna jest równa 2%? Wynik zaokrąglij do 0,01. Jakie jest realne oprocentowanie w tym banku?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
