Bóbr informatyczny (XVIII)

SKRZAT

Zad. 1. Bóbr Bartek ma pięć stempli ponumerowanych od 1 do 5. Użył ich do utworzenia obrazka. W jakiej kolejności użył tych stempli?

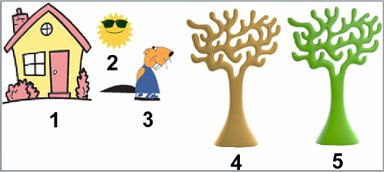
a) 5-2-4-3-1   b) 5-2-3-4-1   c) 5-3-4-2-1   d) 5-4-2-3-1

Zad. 2. Profesorowie wsiadają do autobusu i chcą dojechać do trzech różnych miejsc docelowych. Autobus najpierw zatrzyma się przy lotnisku, następnie przy hotelu, a na końcu przy uniwersytecie. Bagażnik autobusu otwiera się tylko po jednej stronie. Kierowca autobusu chce włożyć walizki profesorów do bagażnika, jedna po drugiej tak, aby przy wysiadaniu można je było wyjąć bez przestawiania pozostałych. Która grupa walizek, powinna być włożona do bagażnika jako ostatnia?
a) profesorów, którzy wysiadają przy uniwersytecie
b) profesorów, którzy wysiadają przy hotelu
c) profesorów, którzy wysiadają na lotnisku
d) Nie ma znaczenia, która grupa walizek zostanie włożona do bagażnika jako ostatnia.

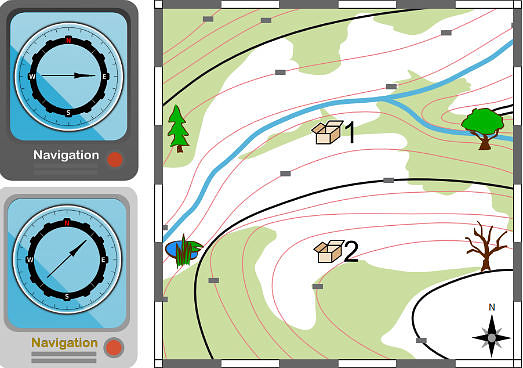
Zad. 3.  Dwoje przyjaciół Ania i Bartek szukają skarbów. Ania szuka skarbu oznaczonego na mapie numerem 1, a Bartek - oznaczonego numerem 2. Przyjaciele stoją w tym samym miejscu, a na swoich telefonach komórkowych, mają uruchomioną nawigację, która pokazuje kierunek, w jakim trzeba iść, aby znaleźć skarb. Ekrany telefonów są widoczne na rysunku, ale nie wiadomo, który telefon jest Ani, a który Bartka. W którym z miejscu na mapie stoją dzieci?

BENIAMIN

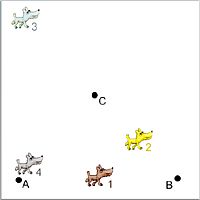
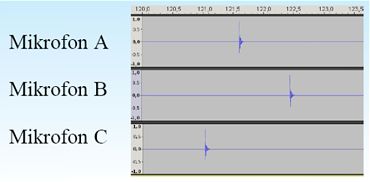
Zad. 1. Trzy mikrofony rozlokowano jak na rysunku. W tej samej chwili zaszczekał jeden z psów. Mikrofony wykryły dźwięk, co zostało pokazane na wykresach. Który pies zaszczekał? 

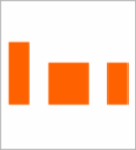
Zad. 2. Z którego zbioru elementów nie można złożyć kwadratu?

Zad. 3. W swoim kraju bobry mają ciekawy zestaw monet:
1 bobrocent, 7 bobrocentów, 12 bobrocentów i 22 bobrocenty. Pracujesz w banku i masz wydać bobrowi kwotę 25 bobrocentów. Jaka jest najmniejsza liczba monet, które użyjesz?

JUNIOR

Zad. 1. Bogdan chce ściąć 7 spośród 9 drzew, które rosną w okręgu w kolejności A, B, C, D, E, F, G, H, I, patrząc zgodnie z kierunkiem ruchu wskazówek zegara. Bogdan stoi przy drzewie A i postanowił postąpić w następujący sposób: najpierw idzie do najbliższego drzew zgodnie z ruchem wskazówek zegara i ścina je. Stamtąd idzie w kierunku przeciwnym do ruchu wskazówek zegara, zatrzymuje się przy drugim w kolejności drzewie i ścina je. Kontynuuje ścinanie drzew na tej samej zasadzie, to znaczy zmienia kierunek przemieszczania się i zwiększa o 1 liczbę opuszczonych drzew, ale ignoruje po drodze te drzewa, które już ściął. Które drzewa nie zostaną w ten sposób ścięte?

Zad. 2. Robotowi można zadać wiele pytań. Może on na nie odpowiedzieć, niekoniecznie zachowując kolejność, ale na każde pytanie udziela tylko jednej odpowiedzi.
Kiedy robot dostaje pytanie, wyświetla na ekranie znak '?', a kiedy udziela odpowiedzi - wyświetla na '!'. Jeśli na ekranie pojawi się ciąg znaków ????!!, to oznacza, że robotowi zadano 4 pytania, a odpowiedział tylko na 2 z nich.

Jeśli robot udziela odpowiedzi, chociaż nie zadano mu pytania, to znaczy, że jest zepsuty. Który z następujących ciągów znaków na ekranie świadczy, że robot nie jest zepsuty? 
a) ????????
b) !???!?!!?!
c) ?!?!!??!??
d) ??!?!!?!!

Zad. 3. Komenda z rys. 1 rysuje sieć kwadratów o 2 rzędach i 5 kolumnach. Komenda z rys. 2 maluje na czerwono 2 kwadraty w pierwszym rzędzie począwszy od trzeciej kolumny.

rys. 1.   

rys. 2.   

Po wykonaniu tych dwóch komend otrzymujemy poniższą sieć.

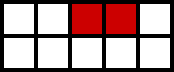
Jaka sieć powstanie po wykonaniu następującego ciągu komend?

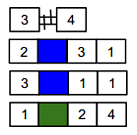
SENIOR

Zad. 1. Bóbr Bartek uwielbia gotować. Jego ulubionym posiłkiem jest chakhokhbili. Podczas gotowania w ogrodzie używa tylko jednego palnika, wykonuje więc poniższe czynności jedna po drugiej:
1. gotowanie cebuli - 10 min
2. gotowanie papryki - 10 min
3. wymieszanie cebuli i papryki, dodanie pomidora i gotowanie tych składników razem - 20 min
4. gotowanie kurczaka - 30 min
5. wymieszanie składników z kroków 3 i 4, dodanie przypraw i gotowanie całości - 20 min
W sumie Bartek potrzebuje 90 minut, aby przygotować chakhokhbili w ogrodzie. Gdy jednak gotuje w domu, ma do dyspozycji tyle palników, ile potrzebuje w danej chwili. Dzieki temu jego danie może być gotowe szybciej. Które z poniższych zdań nie jest prawdziwe?
a) Bartek może skrócić czas o 10 minut, używając 2 palników.
b) Bartek może skrócić czas o 30 minut, używając 2 palników.
c) Bartek może skrócić czas o 40 minut, używając 3 palników.
d) Bartek może skrócić czas o 50 minut, używając 4 palników.

Zad. 2. Bobry dla bezpieczeństwa przesyłają wiadomości zaszyfrowane za pomocą następującego schematu:

Na przykład słowo BEAVER zostanie zaszyfrowane jako WBFCSF.
Bóbr Bartek otrzymał właśnie następującą, zaszyfrowaną wiadomość PMGEP. Jak wygląda ta wiadomość po odszyfrowaniu?

Zad. 3. Listonosz ma za zadanie dostarczyć listy do pięciu domów stojących w szeregu po jednej stronie ulicy. Są ponumerowane od 1 do 5, patrząc od lewej strony. Sąsiednie domy są odległe o 1 km. Listonosz otrzymuje wypłatę za ilość przebytych kilometrów, chce zatem przejść możliwie najdłuższą drogę. Może zaplanować swoją podróż, zaczynając od dowolnego domu i kończąc przy dowolnym z nich, ale musi odwiedzić każdy z domów dokładnie raz i po każdym dostarczeniu listu musi iść bezpośrednio kolejnego domu. W jakiej kolejności listonosz powinien odwiedzić domy?