Strona główna


Podobne nierówności

Przedstawiamy 'kolorowy' dowód nierówności:

$\small \left|\;\sqrt[32]{x^8+4}\ - \ \sqrt[32]{y^8+4}\:\right| \ \ \leq\ \ \left| x-y \right|\ \cdot\ \frac{1}{4\cdot \sqrt[16]{2^3}}\ \ \mbox{ dla } \ x,y\geq0\ .$

Zmodyfikuj go tak, aby otrzymać dowody innych, podobnych nierówności.

Czytaj dalej


Kule w narożach

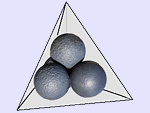Przedstawiamy zadania o kulach umieszczonych w narożach czworościanu foremnego, sześcianu i ośmiościanu foremnego. W przypadku czworościanu pokazujemy niemal pełne rozwiązania. Mamy nadzieję, że dzięki temu Czytelnik nabierze doświadczenia i samodzielne rozwiąże pozostałe zadania.

Czytaj dalej


Z czterech kul

Jaka bryła powstaje z przecięcia czterech jednakowych kul, których środki leżą w odległościach równych promieniowi tych kul? To wydaje się niemożliwe do wyobrażenia, ale warto spróbować. Zobaczcie.

Czytaj dalej


Trójkąty Reuleaux

Jeśli w świecie płaszczaków spojrzeć na koło, to z każdej strony wygląda jednakowo. Precyzyjniej: rzuty prostopadłe koła na dowolne proste są odcinkami tej samej długości. Nie tylko koło (i punkt) mają tę własność. Zobaczcie, jak wyglądają inne takie figury.

1 komentarz Czytaj dalej


Środki par zbiorów

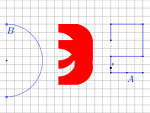Środek odcinka łatwo znaleźć, gdy tylko znamy jego końce. Możemy myśleć, że jest to środek między parą punktów. Gdy końce odcinka będą 'przebiegały' dwa zbiory A i B, środki tych odcinków wypełnią pewną figurę. Jaką? To zależy od A i B. Zobacz, jak dziwne mogą być kształty takich środków między zbiorami.

Czytaj dalej
« pierwsza‹ poprzednia…5678910111213…następna ›ostatnia »

Powrót na górę strony