Prostokąt

Definicja:
Prostokąt to płaski czworokąt równokątny (tzn. ma przystające wszystkie kąty wewnętrzne).

Oznaczenie:
ABCD (czytaj: prostokąt o wierzchołkach A, B, C, D)

Elementy składowe prostokąta:

• punkty A, B, C i D to wierzchołki prostokąta,
• odcinki AB, BC, CD i DA to boki prostokąta,
• odcinki AC i BD to przekątne prostokąta,
• łamana zamknięta ABCDA to brzeg prostokąta,
• długość dłuższego boku to długość prostokąta,
• długość krótszego boku to szerokość prostokąta.

Konstrukcja:

sposób 1	sposób 2
krok:	krok:

Definicje alternatywne:

• równoległobok o przekątnych równej długości,
• równoległobok o przystających kątach wewnętrznych,
• równoległobok, na którym można opisać okrąg,
• równoległobok symetryczny względem odcinka łączącego środki przeciwległych boków,
• trapez prostokątny równoramienny,
• trapez symetryczny względem linii środkowej (tzn. odcinka łączącego środki ramion).

Przykłady:

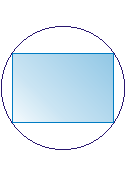
• prostokąt wpisany w okrąg,
• w układzie współrzędnych czworokąt o wierzchołkach: A =(0,0), B=(1,0), C=(1,2), D=(0,2),
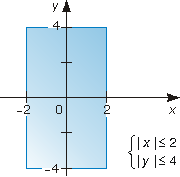
• w układzie współrzędnych rozwiązanie układu nierówności $|x|\leq 2,|y|\leq 4$.

Kontrprzykłady:

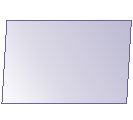
• równoległobok, którego kąty nie są proste,
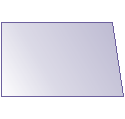
• trapez prostokątny, którego ramiona nie są przystające,
• prostopadłościan - nie jest wielokątem,
• pierścień prostokątny.

Własności:

• na każdym prostokącie można opisać okrąg,
• środkiem okręgu opisanego na prostokącie jest punkt przecięcia przekątnych,
• w każdy prostokąt można wpisać elipsę,
• prostokąt o przystających bokach to kwadrat,
• w prostokąt można wpisać okrąg tylko wtedy, gdy jest on kwadratem,
• prostokąty szczelnie wypełniają płaszczyznę (tworzą parkietaż) i to na wiele sposobów,
• cecha przystawania prostokątów: (bb) - sąsiednie boki są przystające,
• cecha podobieństwa prostokątów: (b/b) - stosunek długości sąsiednich boków jest stały,
• prostokąt można rozciąć na części, z których można ułożyć nowy prostokąt (jest nieskończenie wiele takich możliwości),
• prostokąt można rozciąć na nieprzystające kwadraciki,
• prostokąt ma dwie osie symetrii - łączące środki przeciwległych boków,
• prostokąt NIE MA środka symetrii.

Związki miarowe:

W prostokącie o bokach długości a i b mamy:

• pole P = ab,
• obwód O = 2a + 2b = 2(a+b),
• przekątna d = $\sqrt{a^2+b^2}$,
• kąt wewnętrzny $\alpha$ = 90°,
• suma kątów wewnętrznych wynosi 360°,
• suma kątów zewnętrznych wynosi 360°,
• promień okręgu opisanego R = $\frac{\sqrt{a^2+b^2}}{2}$.

Historia:

• Prostokąt był znany od dawien dawna i wykorzystywany np. w architekturze jako baza wielu budowli. Również działki ziemi wytyczano w kształcie prostokąta.
• Wzór na pole prostokąta (iloczyn długości sąsiednich boków) był znany i stosowany już przez Babilończyków w V tysiącleciu p.n.e. i w starożytnym Egipcie w III tysiącleciu p.n.e.
• Euklides w swoim dziele Elementy z IV w. p.n.e. podaje, że prostokąt to czworobok mający kąty proste, ale nierówne boki. Również irański matematyk Al-Kaszi w dziele Klucz arytmetyki z 1427 roku w części dotyczącej czworokątów wyróżnia prostokąty jako te o równych kątach i nierównych bokach.

Terminy pokrewne:

• prostokątny układ współrzędnych,
• rzut prostokątny,
• prostokąt złoty,
• prostokąt normalny,
• prostokąt łaciński.

Bibliografia:

• Euklides, Elementy, http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
• red. W. Mizerski, Tablice matematyczne, Adamantan, Warszawa 2002.
• Ian Stewart, Histerie matematyczne. Gry i zabawy z matematyką, Prószyński i S-ka, Warszawa 2007.
• W. Więsław, Matematyka i jej historia, Nowik, Opole, 1997.