Janusz Kapusta – polski rysownik, malarz i scenograf od 1981 roku zamieszkały w USA

Czy można wyobrazić sobie, narysować lub skonstruować nieskończoność? Autor książki - artysta plastyk interesujący się filozofią i matematyką - uważa, że tak. Kwintesencją tego pojęcia i wynikiem wieloletnich poszukiwań odpowiedzi na to pytanie jest dla niego pojedynczy, wielościenny kształt (dokładniej rzecz biorąc, 11-ścienny), który opisał w 1985 roku i opatentował w USA pod nazwą K-dron. Jego książka (a raczej album prac i aranżacji) stanowi dokumentację dotyczącą tej bryły, zebraną w okresie dziesięciu lat. Czytelnik krok po kroku wprowadzany jest w świat tajemniczych i zdumiewających własności K-dronu.
Spis treści książki wydaje się dość przewrotny, wygląda bowiem następująco:
1. Zakończenie
2. Odkrycie
3. Droga
4. Opisanie
5. Badanie
6. Zastosowania
7. Wstęp
Taki dziwny układ autor tłumaczy słowami Pascala: na końcu każdego odkrycia pojawia się świadomość, od czego należy rozpocząć opis odkrycia, aby zrozumiał je ktoś inny. Dlatego pierwsze, bogato ilustrowane rozdziały są ciekawą opowieścią o dość przypadkowym odkryciu, które diametralnie zmieniło życie autora. Kolejne - pozwalają przyjrzeć się bliżej konstrukcji i własnościom K-dronu. Autor podaje kilka sposobów otrzymania tej bryły. Najprostszy, to chytre rozcięcie sześcianu na dwa przystające K-drony. Wszystkie konstrukcje zilustrowane są szkicami i zdjęciami modeli.
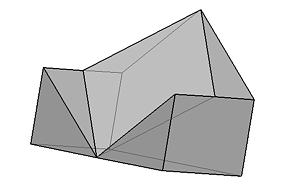 Jednak jeden egzemplarz K-dronu to za mało, bo w pełni docenić jego geometryczne piękno. Dlatego w dalszych rozdziałach autor multiplikuje ten wielościan i składa zeń kolejne bryły, a przez różne kombinacje połączeń i różne kierunki oświetlenia powstałych układów otrzymuje niezwykle różnorodne obiekty. Na tym jednak nie kończą się jego poszukiwania. Zajmuje się również parkietażami przestrzeni, w których wykorzystuje K-drony. Zadziwiające jest to, na ile rozmaitych sposobów można wykorzystać tę niepozorną bryłę i ile zadziwiających obiektów i wzorów z niej stworzyć.
Jednak jeden egzemplarz K-dronu to za mało, bo w pełni docenić jego geometryczne piękno. Dlatego w dalszych rozdziałach autor multiplikuje ten wielościan i składa zeń kolejne bryły, a przez różne kombinacje połączeń i różne kierunki oświetlenia powstałych układów otrzymuje niezwykle różnorodne obiekty. Na tym jednak nie kończą się jego poszukiwania. Zajmuje się również parkietażami przestrzeni, w których wykorzystuje K-drony. Zadziwiające jest to, na ile rozmaitych sposobów można wykorzystać tę niepozorną bryłę i ile zadziwiających obiektów i wzorów z niej stworzyć.
Kapusta sam wymyślił ponad 160 zastosowań K-dronów, np. w budownictwie mogą być wykorzystywane jako betonowe pustaki, kostki brukowe, płytki ścienne, sufitowe i podłogowe luksfery czy dachówki, mogą też służyć jako elementy dekoracyjne - meble, lampy, torby, opakowania, oryginalne elementy biżuterii, zegarki, telefony, zapięcia, a także kształcące wyobraźnię przestrzenną łamigłówki, dziecięce klocki a nawet... globusy.


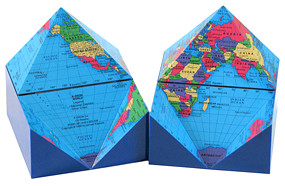

K-dron jest źródłem ciekawych dociekań matematycznych.
- W jaki sposób ułożyć kształt K-dronu z dwunastu przystających ostrosłupów kwadratowych?
- Ile różnych wzorów można otrzymać, składając cztery białe i cztery czarne K-drony w cztery sześciany?
 Książka napisana jest niezwykle przystępnym językiem, dlatego dostępna nawet dla całkowitego matematycznego laika, który dzięki dużej liczbie ilustracji łatwiej może dostrzec i zrozumieć wyjątkowe własności tej niezwykłej bryły opatentowanej w Amerykańskim Urzędzie Patentowym 29 maja 1985 roku pod numerem 4 681 481 jako decorative and functional element for construction and the like (element dekoracyjny i konstrukcyjny w budownictwie itp). Ciekawostką jest, że w 2009 roku w Kole (rodzinnym powiecie Kapusty) odsłonięto pomnik odkrytego przezeń K-dronu, a w 2013 zrobiono to w Wolsztynie.
Książka napisana jest niezwykle przystępnym językiem, dlatego dostępna nawet dla całkowitego matematycznego laika, który dzięki dużej liczbie ilustracji łatwiej może dostrzec i zrozumieć wyjątkowe własności tej niezwykłej bryły opatentowanej w Amerykańskim Urzędzie Patentowym 29 maja 1985 roku pod numerem 4 681 481 jako decorative and functional element for construction and the like (element dekoracyjny i konstrukcyjny w budownictwie itp). Ciekawostką jest, że w 2009 roku w Kole (rodzinnym powiecie Kapusty) odsłonięto pomnik odkrytego przezeń K-dronu, a w 2013 zrobiono to w Wolsztynie.
Jan Kapusta to niezwykły projektant, którego pasja do filozofii zaowocowała fascynującą i wyjątkowo bogatą strukturą nazwaną przez niego K-dronem. Moim jednak zdaniem większa wartość tkwi w odkryciu matematycznym K-dronu niż w jego formie użytkowej wykorzystującej podstawowe symetrie sześcianu, jako np. modułu pozwalającego budować struktury o symetriach sześciennych. Na K-dron można spojrzeć jak na osobliwość w jednorodnej przestrzeni. Janusz Kapusta uczynił wyraźny krok w stronę nieróżniczkowalnej przestrzeni geometrii euklidesowej, w rezultacie czego stworzył K-dron, nowy kształt o fundamentalnym znaczeniu, który łamie symetrię w nieskończonej przestrzeni rozciągającej się nad nim i pod nim.
[Jay Kappraff, matematyk z New Jersey Institute of Technology]




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
