| więcej informacji o tekście: |
|
Do rysunków 3D w niebieskich ramkach użyto apletu www.javaview.de/ Można w nich manipulować myszą. |
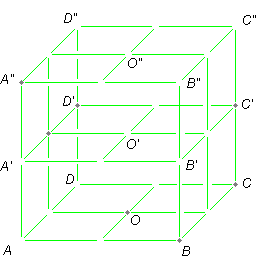
Rzecz będzie się działa w sześcianie o krawędzi długości 2.
Wyróżniamy w nim 27 punktów:
w dolnej podstawie: A, B, C, D - wierzchołki, E, F, G, H - środki boków, O - środek podstawy;
nad nimi, w górnej podstawie: A'', B'', C'', D'', E'', F'', G'', H'', O''
i pomiędzy nimi, po środku: A', B', C', D', E', F', G', H', O'.
Na rysunkach podpisano tylko niektóre z nich. Podpisanie wszystkich sprawiłoby, że rysunek byłby nieczytelny.
Dla pewnej kolekcji K spośród wyróżnionych punktów tego sześcianu niech W = W(K) oznacza najmniejszy wypukły wielościan zawierający punkty z K. Wypukły oznacza: bez dziur i wklęsłości.
Na przykład dla
Ma on:
w = 7 wierzchołków,
k = 13 krawędzi,
s = 8 ścian.
Uwaga: nie wszystkie punkty z K są wierzchołkami (w tym przykładzie nie jest nim O'').
Bryła W ma
objętość V = 6.
Można to obliczyć kilkoma sposobami.
Na przykład tak:
płaszczyzny BDD''B'', CD''B'' rozcinają W na trzy ostrosłupy: dwa o wspólnej podstawie BDD''B'' i trzeci, o podstawie D''B''G'', których objętości można już łatwo obliczyć.
Można też obliczać objętości części sześcianu usuwanych
przy 'rzeźbieniu' W.
Na poniższym rysunku możesz przetestować swoją wyobraźnię przestrzenną.



























Proponujemy kilka zadań.
(Obliczanie objętości bywa żmudne. Te podpunkty można pominąć przy pierwszym podejściu).
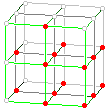 Zadanie 1.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:
Zadanie 1.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
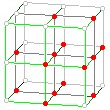 Zadanie 2.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:
Zadanie 2.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
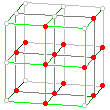 Zadanie 3.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:
Zadanie 3.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 4.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym prawie wszystkie wyróżnione punkty, to znaczy:
a) wszystkie z wyjątkiem: B'', O'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
b) wszystkie z wyjątkiem: B'', C'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
c) wszystkie z wyjątkiem: B'', F'', C'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
d) wszystkie z wyjątkiem: B', B'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
e) wszystkie z wyjątkiem: B, B', B'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
f) wszystkie z wyjątkiem: B', B'', C'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
g) wszystkie z wyjątkiem: B', B'', F'', C'',
to: w = . . . . . k = . . . . . s = . . . . . V = . . . . . .
h) wszystkie z wyjątkiem: B', F', B'', F'', C'',
to: w = . . . . . k = . . . . s = . . . . V = . . . . .
i) wszystkie z wyjątkiem: B', F', C', B'', F'', C'',
to: w = . . . . k = . . . . s = . . . . V = . . . . . .
j) wszystkie z wyjątkiem: B', B'', F'',
to: w = . . . . . k = . . . . . s = . . . . V = . . . . .
Zadanie 5.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym prawie wszystkie wyróżnione punkty, to znaczy:
a) wszystkie z wyjątkiem: B'', O'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
b) wszystkie z wyjątkiem: B'', C'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
c) wszystkie z wyjątkiem: A'', B'', C'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
d) wszystkie z wyjątkiem: A'', E'', B'', C'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
e) wszystkie z wyjątkiem: A'', E'', B'', F'', C'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . .
f) wszystkie z wyjątkiem: A'', E'', B'', F'', C'', G'', D'',
to: w = . . . . k = . . . . s = . . . V = . . . .
Zadanie 6.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty:
a) F, H, A', B', C', D', F'', H'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
b) F, H, A', B', C', D', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
c) F, H, A', B', C', D', F'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
d) F, O, A', B', C', D', O'', H'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
e) E, F, G, H, A', B', C', D', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
f) E, F, G, H, A', B', C', D', O'', E'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
g) E, F, G, H, A', B', C', D', E'', F'', G'', H'',
to: w = . . . . k = . . . . s = . . . . V = . . . .
h) E, F, G, H, A', B', C', D', O'', E'', F'',
to: w = . . . . k = . . . . s = . . . . V = . . . .
Zadanie 7.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty:
a) E, F, G, H, E', F', G', H', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
b) E, F, G, H, E', F', G', H', O'', E'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
c) E, F, G, H, E', F', G', H', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
d) E, G, E', F', G', H', O'', E'', G'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
e) E, G, E', F', G', H', O'', F'', H'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
f) E, E', F', G', H', G'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
g) E, O, E', F', G', H', G'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
h) E, F, O, E', F', G', H', G'', H'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
i) E, B, F, E', F', G', H', G'', D'', H'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
j) E, B, O, E', F', G', H', G'', D'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
k) E, B, F, O, E', F', G', H', G'', D'', H'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
Zadanie 8.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty:
a) A, C, E', F', G', H',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
b) A, C, E', F', G', H', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
c) A, C, E', F', G', H', A'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
d) A, C, E', F', G', H', A'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
e) A, C, E', F', G', H', A'', C'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
f) A, C, E', F', G', H', B'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
g) A, C, E', F', G', H', B'', O'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
h) A, C, E', F', G', H', B'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
Zadanie 9.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty: A, E, O, H, A', E', O', H' oraz
a) punkt B,
to: w = . . . . k = . . . . s = . . . . V = . . . . .
b) punkt F',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
c) punkt F'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
d) punkt C'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
e) punkty B', D',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
f) punkty F', G',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
g) punkty F'', G'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
h) punkty B'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
i) punkty C', F'', G'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
j) punkty C', F'', C'', G'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
k) punkty C', B'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
l) punkty C', B'', C'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
m) punkty C, B'', C'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
n) punkty C, C', B'', F'', G'', D'',
to: w = . . . . k = . . . . s = . . . . V = . . . . .
Zadanie 10.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym
środki wszystkich krawędzi tego sześcianu, to
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 11.
Gdy W jest najmniejszym wypukłym wielościanem zawierającym
środki wszystkich ścian tego sześcianu, to
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 12*. Podaj wszystkie wypukłe wielościany W zawierające pewne spośród punktów A, B, C, D, E, F, G, H, O, A', B', C', D', E', F', G', H', O', A'', B'', C'', D'', E'', F'', G'', H'', O'' tego sześcianu, które mają 16 wierzchołków (w = 16). ** Dlaczego nie ma innych?
Zadanie 13*.
Ile jest wszystkich wypukłych wielościanów W zawierających pewne spośród punktów A, B, C, D, E, F, G, H, O, A', B', C', D', E', F', G', H', O',
A'', B'', C'', D'', E'', F'', G'', H'', O'' tego sześcianu, które spełniają wszystkie poniższe warunki:
mają 6 wierzchołków (w = 6),
zawierają punkty B, D, B'', D'',
płaszczyzna BB''D'' jest płaszczyzną symetrii.
Zadanie 14*.
Ile jest wszystkich wypukłych wielościanów W zawierających pewne spośród punktów A, B, C, D, E, F, G, H, O, A', B', C', D', E', F', G', H', O',
A'', B'', C'', D'', E'', F'', G'', H'', O'' tego sześcianu, które spełniają wszystkie poniższe warunki:
mają 6 wierzchołków (w = 8),
zawierają punkty B, D, B'', D'',
płaszczyzna O'' jest środkiem symetrii.
Zadanie 15**. Niech W będzie najmniejszym wypukłym wielościanem zawierającym pewne spośród punktów A, B, C, D, E, F, G, H, O, A', B', C', D', E', F', G', H', O', A'', B'', C'', D'', E'', F'', G'', H'', O'' tego sześcianu.
a) Jaka może być liczba w jego wierzchołków?
b) Jaka może być liczba k jego krawędzi?
c) Jaka może być liczba s jego ścian?
d) Jaka jest najmniejsza (niezerowa) objętość V ?
Określenie. Powiemy, że dwa wielościany mają ten sam typ, jeśli mają jednakowe liczby: wierzchołków, krawędzi, ścian, ścian trójkątnych, ścian czworokątnych, ścian pięciokątnych, ścian sześciokątnych, ścian siedmiokątnych,... .
Zadanie 16. Podaj wszystkie typy wielościanów wypukłych zawierających 8 wierzchołków sześcianu i jeszcze jeden dodatkowy punkt X.
Zadanie 17**. Podaj wszystkie typy wielościanów wypukłych zawierających wszystkie 2n wierzchołki graniastosłupa prawidłowego (o podstawie n-kąta foremnego) i jeszcze jeden dodatkowy punkt X.
Zadanie 18. Podaj wszystkie typy wielościanów wypukłych zawierających 4 wierzchołki czworościanu foremnego i jeszcze jeden dodatkowy punkt X.
Zadanie 19**. Podaj wszystkie typy wielościanów wypukłych zawierających wszystkie n+1 wierzchołków ostrosłupa prawidłowego (o podstawie n-kąta foremnego) i jeszcze jeden dodatkowy punkt X.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
