KĄCIK NAUKOWY › Kółko matematyczne

Wypukłe wielościany w graniastosłupie

Data ostatniej modyfikacji:
2013-06-6
Autor: 
Krzysztof Omiljanowski
pracownik IM UWr
Poziom edukacyjny: 
gimnazjum
szkoła średnia z maturą
szkoła profilowana zawodowa
Dział matematyki: 
geometria syntetyczna
geometria przestrzenna
Do rysunków 3D w niebieskich ramkach
użyto apletu www.javaview.de/
Można w nich manipulować myszą.


 

Rzecz będzie się działa w graniastosłupie prawidłowym o wysokości OO'' = 2 i podstawach ABCDEF oraz A''B''C''D''E''F'', których boki mają długość 1. Niech A', B', C',... oznaczają środki krawędzi odpowiednio: AA'', BB'', CC'',... i niech O' oznacza środek wysokości OO''.

Dla pewnej kolekcji K wyróżnionych punktów graniastosłupa, niech W = W(K) oznacza najmniejszy wypukły wielościan zawierający punkty z kolekcji K. Wypukły oznacza: bez dziur i wklęsłości.

 

Na przykład gdy K składa się z punktów

O, A, B, C, E, A', C', A'', B'', E'', F'',
wielościan W pokazany jest na rysunku.
Ma on:
    w = 9 wierzchołków,
    k = 16 krawędzi,
    s = 9 ścian.
Uwaga: nie wszystkie punkty z K są wierzchołkami W (np. O, A').

Bryła W ma objętość V = 13 / 6. Można to obliczyć kilkoma sposobami. Na przykład tak: wielokąty AEE''A'', BEE''B'', B'C'E' rozcinają W na dwa graniastosłupy i dwa ostrosłupy (których objętości nietrudno obliczyć).
lub tak: obliczamy objętości części graniastosłupa usuwanych przy 'rzeźbieniu' W.

             
bryła W          anty:

 

Na poniższym rysunku możesz przetestować swoją wyobraźnię przestrzenną.

 

Wyobraź sobie najmniejszy wypukły wielościan W zawierający zaznaczone czerwone punkty graniastosłupa.
Klikając w punkty, możesz zmieniać ich kolor. W ten sposób sam wybierzesz kolekcję K.
                 
W ma: 12 wierzchołków, 19 krawędzi, 9 ścian,
w tym: trójkątnych 3, czworokątnych 2,
pięciokątnych 3, szesciokątnych 1 bryła W          anty:

 

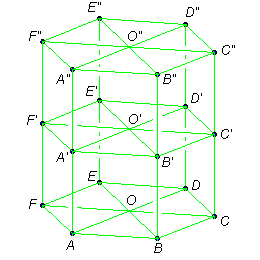
Proponujemy jeszcze kilka zadań. Uwaga, obliczanie objętości bywa żmudne.

 

Zadanie 1.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to

      w = . . . . . .       k = . . . . . .       s = . . . . . .       V = . . . . . .    

Zadanie 2.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym zaznaczone na rysunku punkty, to:

      w = . . . . . .       k = . . . . . .       s = . . . . . .       V = . . . . . .    

Zadanie 3.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, C', F', A'', B'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, A', B', F', A'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, A', B', F', B'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, A', B', F', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, A', B', F', D'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .

Zadanie 4.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, C, D, E, F, O, A'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, B, C, D, E, F, O, A'', B'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, C, D, E, F, O, A'', C'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, B, C, D, E, F, O, A'', D'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  e)  A, B, C, D, E, F, O, A', B', C', D', E', F', O', A'', D'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  f)  A, B, C, D, E, F, O, A', B', C', D', E', F', O', A'', B'', D'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
 

Zadanie 5.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, O, A', B', O', A'', B'', 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, B, C, O, A', B', C', O', A'', B'', C'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, C, O, A', B', C', O', O'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, B, C, O, A', B', C', O', O'', B'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  e)  A, B, C, O, B', O', O'', B'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  f)  A, B, C, O, A', B', O', A'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
 

Zadanie 6.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, C, D, E, F, O, O', A', B', D', E' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, B, C, D, E, F, O, O', A', B', D', E', O'', A'', B'', D'', E'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, C, D, E, F, O, O', A', B', D', E', O'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, B, C, D, E, F, O, O', C', D', E', F' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  e)  A, B, C, D, E, F, O, O', C', D', E', F', O'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .

Zadanie 7.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, C, D, E, F, A', B', C', D', E', F', A'', B'', D'', E'', F'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, C, D, E, F, A', B', C', D', E', F', A'', B'', D'', E'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, D, E, A', B', C', D', E', F', A'', B'', D'', E'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, B, D, E, A', B', C', D', E', F', B'', C'', E'', F'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  e)  A, B, D, E, A', B', C', D', E', F', B'', C'', E'', F'' , 
          to    w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .

Zadanie 8.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, O, O', O'', A'', B'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, B, O, O', O'', B'', C'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, O, O', O'', C'', D'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, B, O, O', O'', D'', E'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  e)  A, B, O, O', O'', E'', F'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .

Zadanie 8'.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, C, O, O', O'', A'', B'', C'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, B, C, O, O', O'', B'', C'', D'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, C, O, O', O'', C'', D'', E'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, B, C, O, O', O'', D'', E'', F'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .

Zadanie 8''.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, B, C, D, O, O', O'', A'', B'', C'', D'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, B, C, D, O, O', O'', B'', C'', D'', E'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, B, C, D, O, O', O'', C'', D'', E'', F'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .

Zadanie 9.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym punkty
 
  a)  A, O, B', O', C'', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  b)  A, O, C', O', E'', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  c)  A, O, C', O', D'', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  d)  A, D, O, B', E', O', C'', F'', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  e)  A, D, O, B', E', O', B'', E'', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
  f)  A, O, B', F', A'', O'' ,  to   w = . . . . .   k = . . . . .   s = . . . . .  V = . . . . . .
 
 

Zadanie 10.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym środki wszystkich krawędzi tego graniastosłupa, to
          w = . . . . . .       k = . . . . . .       s = . . . . . .       V = . . . . . .    

Zadanie 11.   Gdy W jest najmniejszym wypukłym wielościanem zawierającym środki wszystkich ścian tego graniastosłupa, to
          w = . . . . . .       k = . . . . . .       s = . . . . . .       V = . . . . . .    

Zadanie 12**.   Niech W będzie najmniejszym wypukłym wielościanem zawierającym pewne spośród punktów A, B, C, D, E, F, O, A', B', C', D', E', F', O', A'', B'', C'', D'', E'', F'', O'' tego graniastosłupa.

   a)   Jaka może być liczba w jego wierzchołków?

   b)   Jaka może być liczba k jego krawędzi?

   c)   Jaka może być liczba s jego ścian?

   d)   Jaka jest najmniejsza (niezerowa) objętość V?

 

 

Powrót na górę strony