|
Do rysunków 3D użyto apletu
www.javaview.de/
Można w nich manipulować myszą. |
Poniższe cztery powierzchnie utworzono według jednakowego schematu:
- każda mieści się w cylindrze (o promieniu 1),
- każda jest zbudowana z patyków - odcinków zaczepionych jednym końcem w środku podstawy cylindra,
- drugie końce tych patyków sięgają do powierzchni bocznej cylindra.
Najlepiej widać to na pierwszym rysunku. Sprawdź.
Patrząc z góry, można zauważyć, że nad każdą 'szprychą' w podstawie cylindra jest dokładnie jeden patyk.
Przepis na taką powierzchnię jest następujący:
nad/pod 'szprychą' w podstawie, która tworzy z osią OX kąt x . 360o,
zaczepiamy w środku podstawy patyk, którego drugi koniec
leży na powierzchni cylindra na wysokości f (x).
Ogólnie nazwijmy takie powierzchnie f-stożkami.
Według podobnego schematu określamy powierzchnie, które nazwiemy anty-f-stożkami:
każda taka powierzchnia zawarta jest w cylindrze (o promieniu 1) i jest zbudowana z patyków - odcinków zaczepionych jednym końcem w osi cylindra, których drugie końce leżą na okręgu podstawy cylindra.
A dokładniej:
nad/pod 'szprychą' w podstawie cylindra, która tworzy z osią OX kąt x . 360o,
zaczepiamy w osi cylindra patyk na wysokości f (x),
a jego drugi koniec zaczepiamy na brzegu podstawy cylindra (na poziomie 0).
ZADANIE 1. Dla podanych niżej funkcji
a) znajdź pary f-stożków podobnych (w potocznym znaczeniu tego słowa),
b) znajdź pary anty-f-stożków podobnych (w potocznym znaczeniu tego słowa).
f1(x) =
sin(x . 4 ) / 2
f2(x) = sin2(x . 4 ) - 1/2
f3(x) = sin(x . 6 ) / 2
f4(x) = cos2(x . 6 ) -1/2
|
f5(x) =
sin(x . 2) / 2
f6(x) = sin(x . 3 ) / 2
f7(x) = cos(x . 3 ) / 2
f8(x) = | sin(x . 3 ) |
|
f9(x) =
sin2(x . 3) - 1/2
f10(x) = | sin(x . 2 ) |
f11(x) = 64x(x - 0,25)(x - 0,75)(x - 1) f12(x) = | 20x(x - 0,5)(x - 1) | - 1/2 |
Rozważmy teraz funkcje f, które na przedziale [0, 1] przyjmują tylko wartości nieujemne.
Określamy f-bryłę następująco:
jest ograniczona od dołu przez podstawę cylindra (o promieniu 1), od góry przez powierzchnię f-stożka, a 'z boków' przez powierzchnię cylindra.
Podobnie określamy anty-f-bryłę:
jest ograniczona od dołu przez podstawę cylindra (o promieniu 1), a od góry przez powierzchnię anty-f-stożka.
Dla funkcji stałej f (x) = 1 mamy oczywiście (dlaczego oczywiście?):
/3,objętość anty-f-bryły jest równa
/3.Dla niektórych innych funkcji też można łatwo znaleźć objętości ich f-brył i anty-f-brył.
Na poniższym rysunku f-bryła i anty-f-bryła podzielone są na sektory.
Pokazany też jest dokładnie pierwszy sektor, o wysokości mniej więcej f(0).
Inne sektory wyglądają podobnie.
bryła: sektor:
Przyglądając się pojedynczemu sektorowi f-bryły i anty-f-bryły (dla tej samej funkcji f), można zobaczyć tezę poniższego twierdzenia.
Twierdzenie A
Dla dowolnej funkcji f (o wartościach nieujemnych)
Można też zauważyć, że powierzchnia boczna f-bryły (zawarta w powierzchni bocznej cylindra) jest niemal taka sama, jak powierzchnia pod wykresem funkcji f.
'Niemal' oznacza, że trzeba rozciągnąć w poziomie powierzchnię pod wykresem funkcji (rozciągając ją 2 razy), by móc ją nakleić na powierzchnię boczną f-bryły.
Przyglądając się pojedynczemu sektorowi f-bryły,
można zobaczyć, że jest to niemal ostrosłup o wierzchołku w środku podstawy cylindra, którego wysokością jest promień podstawy cylindra (=1) i którego podstawą jest (niemal) trapez.
Ten trapez jest 2 razy
szerszy od odpowiadającego mu paska powierzchni pod wykresem f.
Stąd widać tezę poniższego twierdzenia.
Twierdzenie B
Dla dowolnej funkcji f (o wartościach nieujemnych),
gdy A oznacza pole powierzchni pod wykresem funkcji f (na przedziale [0,1]), to
ZADANIE 2. Dla poniższych funkcji f oblicz objętość:
a) f-bryły,
b) anty-f-bryły.
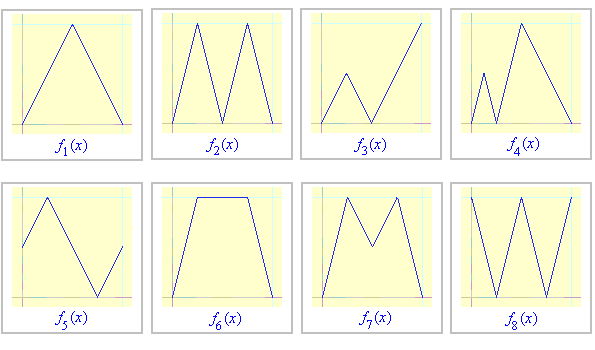
ZADANIE 3. Dla których z poniższych funkcji fk objętość fk-bryły jest:
/3?
b) równa 2/3?
c) większa od 2/3?
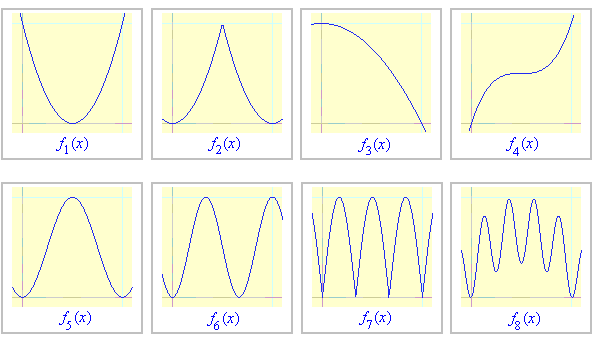
ZADANIE 4. Czy istnieje jakaś zależność pomiędzy objętością f-bryły a objętością bryły pod f-schodami?
Jeśli zainteresował Cię ten temat, zajrzyj koniecznie do kolejnych artykułów: Szprychy w cylindrze (3) - f-abażury oraz Szprychy w cylindrze (4) - f-ślimaki.
