Równania z dwiema niewiadomymi zawierają dwie zmienne, zwykle oznaczone jednymi z ostatnich liter alfabetu, np. x i y. Równania liniowe (nazywane też równaniami stopnia pierwszego) to takie równania, w których wszystkie niewiadome występują co najwyżej w pierwszej potędze. Zatem równania liniowe z dwiema niewiadomymi wyglądają tak:
ax + by + c = 0,
gdzie a, b, c oznaczają dane współczynniki liczbowe, przy czym przynajmniej jedna z liczb a i b jest różna od zera.
Czasem równanie liniowe z dwiema niewiadomymi mają taki sam zapis, jak równanie liniowe z jedną niewiadomą, np. 2x+3y = 3y-7 jest równoważne równaniu 2x=-7. W treści zadania musi wtedy znaleźć się informacja, ile zmiennych ma to równanie, gdyż w przeciwnym razie, może ono nie dać się rozwiązać (nie będziemy wiedzieli, czy pierwiastkami mają być liczby, czy pary liczb).
Przykłady
- 2x + 5y + 7 = 0
- x + y = 0
- -x = 8y
- 3y - 11 $\sqrt{2}$x
- $\frac{x + y}{2} = 3$
- 5x + 2y-5 = 2y+5
Kontrprzykłady
- $\frac{2}{x + y} = 3$ (to nie jest równanie liniowe)
- x2 + y2 = 25 (to nie jest równanie liniowe)
- 5 = 0 (to nie jest równanie liniowe)
- x + y + z = 0 (to nie jest równanie z dwiema niewiadomymi)
- 12x - 15(y-3) = 15x + 12(z + 3) (to nie jest równanie z dwiema niewiadomymi)
Rozwiązywanie równań liniowych z dwiema niewiadomymi
Najpierw doprowadzamy równanie do postaci ax + by + c = 0, a potem stosujemy metodę równań równoważnych. W zależności od tego, które ze współczynników a i b są różne od zera, postępujemy według jednego z poniższych schematów.
1) a=0 i b≠0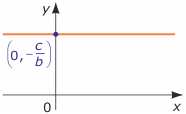
Otrzymujemy równanie liniowe 0x+by+c =0, które nie zależy od x. Stąd y = - $\frac{c}{b}$. Zatem pierwiastkiem równania jest każda para liczb postaci (r, - $\frac{c}{b}$), gdzie r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich par, czyli {(r, - $\frac{c}{b}$) : r$\in$R}. Jest to prosta pozioma prostopadła do osi OY w punkcie (0, - $\frac{c}{b}$).
2) a≠0 i b=0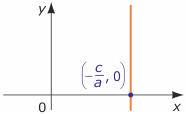
Otrzymujemy równanie liniowe ax+0y+c =0, które nie zależy od y. Stąd x = - $\frac{c}{a}$. Zatem pierwiastkiem równania jest każda para liczb postaci (- $\frac{c}{a}$, r), gdzie r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich par, czyli {(- $\frac{c}{b}$, r) : r$\in$R}. Jest to prosta pionowa prostopadła do osi OX w punkcie (- $\frac{c}{a}$, 0).
3) a≠0 i b≠0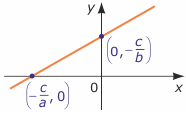
Przekształcamy równanie do postaci równoważnej
y = - $\frac{a}{b}$x - $\frac{c}{b}$. Pierwiastkiem tego równania jest każda para liczb postaci (r, - $\frac{a}{b}$r - $\frac{c}{b}$), gdzie r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich par, czyli {(r, - $\frac{a}{b}$r - $\frac{c}{b}$) : r$\in$R}. Jest to prosta, która przecina oś OX w punkcie (- $\frac{c}{a}$, 0), a oś OY w punkcie (0, - $\frac{c}{b}$).
Uwaga dla licealistów: można powiedzieć, że jest to prosta pochylona do osi OX pod kątem, którego tangens wynosi - $\frac{a}{b}$.
Przykłady
Rozwiąż równania z dwiema niewiadomymi.
1) y + 2x - 1 = 0
Rozwiązanie
y + 2x - 1 = 0 /+1
y + 2x = 1 /-2x
y = -2x + 1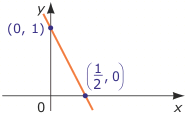
Pierwiastkiem równania jest każda para liczb postaci (r, -2r+1), gdzie r jest dowolną liczbą rzeczywistą, np. pierwiastkami tego równania są pary (0, 1), (1, -1), (-1, 3) ($\frac{1}{2}$, 0) i inne. Rozwiązaniem równania są wszystkie takie pary, czyli zbiór
{(r, -2r+1) : r$\in$R}. Pary te tworzą na płaszczyźnie prostą, przechodzącą przez punkty na osiach: (0, 1) i ($\frac{1}{2}$, 0).
2) 63x - 7y + 14 = 0
Rozwiązanie
63x - 7y + 14 = 0 /:7
9x - y + 2 = 0 /-(9x + 2)
-y = -9y - 2 /·(-1)
y = 9x + 2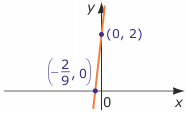
Pierwiastkiem równania jest każda para liczb postaci (r, 9r+2), gdzie r jest dowolną liczbą rzeczywistą, np. pierwiastkami tego równania są pary (0, 2), (1, 11), (-1, -7) (- $\frac{2}{9}$, 0) i inne. Rozwiązaniem równania są wszystkie takie pary, czyli zbiór
{(r, 9r+2) : r$\in$R}. Pary te tworzą na płaszczyźnie prostą, przechodzącą przez punkty na osiach: (0, 2) i (- $\frac{2}{9}$, 0).
3) 0,5y = 11
Rozwiązanie
0,5y = 11 /:0,5
y = 22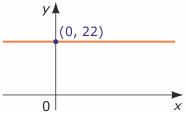
Pierwiastkiem równania jest każda para liczb postaci (r, 22), gdzie r jest dowolną liczbą rzeczywistą, np. pierwiastkami tego równania są pary (0, 22), (1, 22), (-1, 22), ($\pi$, 22) i inne. Rozwiązaniem równania są wszystkie takie pary, czyli zbiór
{(r, 22) : r$\in$R}. Pary te tworzą na płaszczyźnie prostą poziomą przechodzącą przez punkt (0, 22).
4) 0,5x = 11
Rozwiązanie
0,5x = 11 /:0,5
x = 22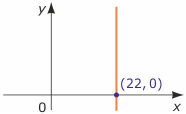
Pierwiastkiem równania jest każda para liczb postaci (22, r), gdzie r jest dowolną liczbą rzeczywistą, np. pierwiastkami tego równania są pary (22, 0), (22, 1), (22, -1), (22,$\pi$) i inne. Rozwiązaniem równania są wszystkie takie pary, czyli zbiór {(22, r) : r$\in$R}. Pary te tworzą na płaszczyźnie prostą pionową przechodzącą przez punkt (22, 0).
5) (x - 1) + 3(x - 1) + 5(x - 1) + 7(x - 1) = -16
Rozwiązanie
(x - 1) + 3(x - 1) + 5(x - 1) + 7(x - 1) = -16 wyłączamy wspólny czynnik przed nawias
(x - 1)(1 + 3 + 5 + 7) = -16 wykonujemy dodawanie w II nawiasie
(x - 1)·16 = -16 /:16
x - 1 = -1 /+1
x = 0
Pierwiastkiem równania jest każda para liczb postaci (0, r), gdzie r jest dowolną liczbą rzeczywistą, np. pierwiastkami tego równania są pary (0, 0), (0, 1), (0, -1), (0, -117), (0, $\pi$) i inne. Rozwiązaniem równania są wszystkie takie pary, czyli zbiór {(0, r) : r$\in$R}. Pary te tworzą na płaszczyźnie oś OY.
6) 2(x+y) = 2x + 2y
Rozwiązanie
Równanie to jest równoważne równaniu stopnia zero z dwiema niewiadomymi 0 = 0. Jest to równanie tożsamościowe, którego pierwiastkiem jest każda para (p, r) liczb rzeczywistych, a rozwiązaniem jest zbiór wszystkich takich par, czyli R2 = {(p, r) : p, r$\in$ R}. Pary te tworzą całą płaszczyznę.
7) 2x + y = 2x + y +7
Rozwiązanie
Równanie to jest równoważne równaniu stopnia zero z dwiema niewiadomymi 0 = 7. Jest to równanie sprzeczne, które nie ma pierwiastków, a jego rozwiązaniem jest zbiór pusty $\emptyset$.
A teraz spróbuj sam
1) Wskaż równania liniowe z dwiema niewiadomymi. Dlaczego odrzuciłeś pozostałe?
- x + y + 1 = 0
- 3 x + y + 1 = 30
- x + 2y + 3 = 3x + 2y + 1
- $\frac{1}{x}-\frac{1}{y} = 5$
- y - 7 = z
- 0,5 + y1 - 2,5y2 = 3,5x
2) Rozwiąż poniższe równania i podaj ich pierwiastki.
- y = x
- 2x + 2y = 2x - y
- x - y + 2x + y + 3x - y + 4x + y = 5
- x + 2y - 5 = 0
- $\frac{2x + 6 - 3y}{6} - \frac{x}{3} = 6 - 0,5y$
- y - x = -(x - y)
Równania liniowe z trzema niewiadomymi wyglądają podobnie do tych z dwiema niewiadomymi, ale dodatkowo zawierają trzecią zmienną, oznaczoną np. literą z. Równania te mają zatem postać:
ax + by + cz + d = 0,
gdzie a, b, c, d oznaczają dane współczynniki liczbowe, przy czym przynajmniej jedna z liczb a, b i c jest różna od zera.
Czasem równanie liniowe z trzema niewiadomymi ma taki sam zapis, jak równanie liniowe z jedną niewiadomą (np. 2x+3y-z = 3y-7-z jest równoważne równaniu 2x=-7) albo z dwiema niewiadomymi (np. równanie (2x+3y+z=z+1 jest równoważne równaniu 2x+3y=1). W treści zadania musi wtedy znaleźć się informacja, ile zmiennych ma to równanie, gdyż w przeciwnym razie, może ono nie dać się rozwiązać (nie będziemy wiedzieli, czy pierwiastkami mają być liczby, pary liczb, czy trójki liczb).
Przykłady
- x + 2y + 3z + 4 = 0
- z = 11x + 0,11y
- x + y + z = x + y + 2z
- $\frac{x + 4}{3} = \frac{1}{9}(z + 2y + 3x)$
Kontrprzykłady
- x + y + z + t + 1 = 0 (to nie jest równanie z trzema niewiadomymi)
- 3x1 - 6x2 + 9x3 - 12y + 15z = 0,3 (to nie jest równanie z trzema niewiadomymi)
- x2 + y2 + z2 = 32 (to nie jest równanie liniowe)
- $\frac{1}{x} + 2y + 3z + 4 = 0$ (to nie jest równanie liniowe)
- xyz = 7·8·9 (to nie jest równanie liniowe)
Rozwiązywanie równań liniowych z trzema niewiadomymi
Najpierw doprowadzamy równanie do postaci ax + by + cz + d = 0, a potem stosujemy metodę równań równoważnych. W zależności od tego, które ze współczynników a, b i c są różne od zera, postępujemy według jednego z poniższych schematów.
1) a=0, b=0, c≠0
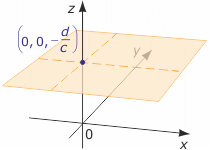Otrzymujemy równanie liniowe 0x+0y+cz+d =0, które nie zależy od x ani od y. Stąd z = - $\frac{d}{c}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (p, r, - $\frac{d}{c}$), gdzie
p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(p, r, - $\frac{d}{c}$) : p, r$\in$R}. Jest to płaszczyzna pozioma prostopadła do osi OZ w punkcie (0, 0, - $\frac{d}{c}$).
2) a=0, b≠0, c=0
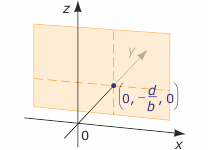Otrzymujemy równanie liniowe 0x+by+0z+d =0, które nie zależy od x ani od z. Stąd y = - $\frac{d}{b}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (p, - $\frac{d}{b}$, r), gdzie
p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(p, - $\frac{d}{b}$, r) : p, r$\in$R}. Jest to płaszczyzna pionowa prostopadła do osi OY w punkcie (0, - $\frac{d}{b}$, 0).
3) a≠0, b=0, c=0
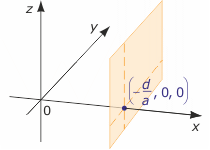Otrzymujemy równanie liniowe ax+0y+0z+d =0, które nie zależy od y ani od z. Stąd x = - $\frac{d}{a}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (- $\frac{d}{a}$, p, r), gdzie
p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(- $\frac{d}{a}$, p, r) : p, r$\in$R}. Jest to płaszczyzna pionowa prostopadła do osi OX w punkcie (- $\frac{d}{a}$, 0, 0).
4) a=0, b≠0, c≠0
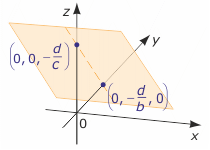Otrzymujemy równanie liniowe 0x+by+cz+d =0, które nie zależy od x. Stąd z = - $\frac{b}{c}y-\frac{d}{c}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (p, r, - $\frac{b}{c}r-\frac{d}{c}$), gdzie p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(p, r, - $\frac{b}{c}r-\frac{d}{c}$) : p, r$\in$R}. Jest to płaszczyzna równoległa do osi OX, przecinająca oś OY w punkcie (0, - $\frac{d}{b}$, 0), a oś OZ w punkcie (0, 0, - $\frac{d}{c}$), czyli przecinająca płaszczyznę YZ wzdłuż prostej o równaniu by+cz+d = 0.
5) a≠0, b=0, c≠0
Otrzymujemy równanie liniowe ax+0y+cz+d =0, które nie zależy od y. Stąd z = - $\frac{a}{c}y-\frac{d}{c}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (p, r, - $\frac{a}{c}p-\frac{d}{c}$), gdzie p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(p, r, - $\frac{a}{c}p-\frac{d}{c}$) : p, r$\in$R}. Jest to płaszczyzna równoległa do osi OY, przecinająca oś OX w punkcie (- $\frac{d}{a}$, 0, 0) a oś OZ w punkcie (0, 0, - $\frac{d}{c}$), czyli przecinająca płaszczyznę XZ wzdłuż prostej o równaniu ax+cz+d = 0.
6) a≠0, b≠0, c=0
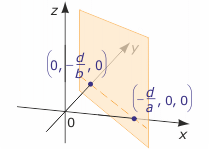Otrzymujemy równanie liniowe ax+by+0z+d =0, które nie zależy od z. Stąd y = - $\frac{a}{b}y-\frac{d}{b}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (p, - $\frac{a}{b}p-\frac{d}{b}$, r), gdzie p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(p, - $\frac{a}{b}p-\frac{d}{b}$, r) : p, r$\in$R}. Jest to płaszczyzna pionowa przecinająca oś OX w punkcie (- $\frac{d}{a}$, 0, 0), a oś OY w punkcie (0, - $\frac{d}{b}$, 0), czyli przecinająca płaszczyznę XY wzdłuż prostej o równaniu ax+by+d = 0.
7) a≠0, b≠0, c≠0
Przekształcamy równanie do postaci z = - $\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}$. Zatem pierwiastkiem równania jest każda trójka liczb postaci (p, r, - $\frac{a}{c}p-\frac{b}{c}r-\frac{d}{c}$), gdzie p, r$\in$R wybieramy dowolnie. Rozwiązaniem równania jest zbiór wszystkich takich trójek, czyli zbiór
{(p, r, - $\frac{a}{c}p-\frac{b}{c}r-\frac{d}{c}$) : p, r$\in$R}.
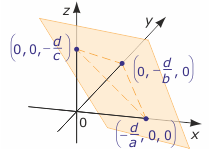Jest to płaszczyzna położona w przestrzeni w ogólny sposób (nierównoległa do żadnej z osi układu współrzędnych) przecinająca oś OX w punkcie
(- $\frac{d}{a}$, 0, 0), oś OY w punkcie (0, - $\frac{d}{b}$, 0), a oś OZ w punkcie (0, 0, - $\frac{d}{c}$), czyli przecinająca płaszczyznę XY wzdłuż prostej o równaniu ax+by+d = 0, płaszczyznę XZ wzdłuż prostej o równaniu ax+cz+d = 0 i płaszczyznę YZ wzdłuż prostej o równaniu by+cz+d = 0.
Przykłady
Rozwiąż równania z trzema niewiadomymi.
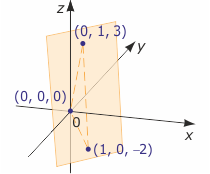
1) 5z - 5 = 15y - 10x - 5
Rozwiązanie
5z - 5 = 15y - 10x - 5 /+5
5z = 15y - 10x /:5
z = 3y - 2x
Pierwiastkiem równania jest każda trójka liczb postaci (p, r, 3r-2p), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, 0, 0), (0, 1, 3), (1, 0, -2), (1, 1, 1) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(p, r, 3r-2p) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę przechodzącą przez początek układu (0, 0, 0) i punkty: (0, 1, 3) i (1, 0, -2).
2) 1000 + 100x + 10y + z = 0
Rozwiązanie
1000 + 100x + 10y + z = 0 /-z
1000 + 100x + 10y = -z /:(-1)
-1000 - 100x - 10y = z
z = -100x - 10y - 1000
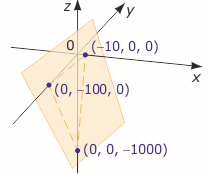Pierwiastkiem równania jest każda trójka liczb postaci (p, r, -100p - 10r - 1000), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, 0, -1000), (0, -100, 0), (-10, 0, 0), (-9, -9, -10) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(p, r, -100p - 10r - 1000) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę przecinającą osie układu współrzędnych w punktach (-10, 0, -0), (0, -100, 0), (0, 0, -1000).
3) 2x + 3y + 4x + 5y = 2z + 4 + 8y
Rozwiązanie
2x + 3y + 4x + 5y = 2z + 4 + 8y lewa strona: grupujemy wyrazy podobne
(2x + 4x) + (3y + 5y) = 2z + 4 + 8y lewa strona: wykonujemy działania w nawiasach
6x + 8y = 2z + 4 + 8y /-8y
6x = 2z + 4 /:2
3x = z + 2 /-2
z = 3x - 2
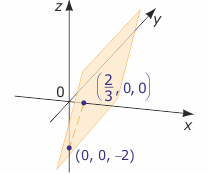Pierwiastkiem równania jest każda trójka liczb postaci (p, r, 3p-2), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, 0, -2), (2/3, 0, 0),
(0, 17, -2), (2/3, √3, 0) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(p, r, 3p-2) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę równoległą do osi OY i przechodzącą przez następujące punkty na pozostałych osiach: (0, 0, -2) i (2/3, 0, 0).
4) x + y + z = x + 1
Rozwiązanie
x + y + z = x + 1 /-(x + y)
z = -y + 1
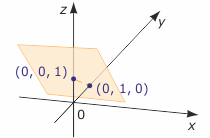Pierwiastkiem równania jest każda trójka liczb postaci (p, r, -r + 1), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, 0, 1), (0, 1, 0),
(5, 0, 1), (-2, 1, 0) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(p, r, -r + 1) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę równoległą do osi OX i przechodzącą przez następujące punkty na pozostałych osiach: (0, 1, 0) i (0, 0, 1).
5) -3(x - y - z) - 3(1 - 1/3x + z) = 0
Rozwiązanie
-3(x - y - z) - 3(1 - 1/3x + z) = 0 lewa strona: wyłaczamy wspólny czynnik przed nawias
(-3)(x - y - z + 1 - 1/3x + z) = 0 lewa strona: grupujemy wyrazy podobne
(-3)((x - 1/3x) + (-z + z) - y + 1) = 0 lewa strona: redukujemy wyrazy podobne
(-3) (2/3x - y + 1) = 0 /:(-3)
2/3x - y + 1 = 0 /+y
2/3x + 1 = y
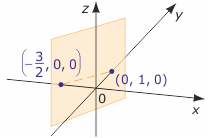Pierwiastkiem równania jest każda trójka liczb postaci (p, 2/3p + 1 , r), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, 1, 0), (-3/2, 0, 0), (0, 1, -17), (3, 3, $\sqrt{2}$) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(p, 2/3p + 1, r) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę równoległą do osi OZ i przechodzącą przez następujące punkty na pozostałych osiach: (-3/2, 0, 0) i (0, 1, 0).
6) 9x + 3√3y + 3z = 3(z + √3(y + 1))
Rozwiązanie
9x + 3√3y + 3z = 3(z + √3(y + 1)) /:3
3x + √3y + z = z + √3(y + 1) prawa strona: wykonujemy mnożenie
3x + √3y + z = z + √3y + √3 /-(√3y + z)
3x = √3 /:3
x = √3/3
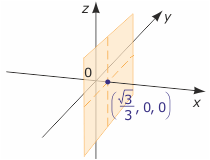Pierwiastkiem równania jest każda trójka liczb postaci (√3/3, p, r), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (√3/3, 0, 0), (√3/3, 2, -3),
(√3/3, √2, -1/2) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(√3/3, p, r) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę pionową prostopadłą do osi OX, przechodzącą przez punkt o współrzędnych (√3/3, 0, 0).
7) $\frac{z + 1}{2} + \frac{x + 2}{3} + \frac{y + 3}{4} = \frac{4x + 3y}{12}$
Rozwiązanie
$\frac{z + 1}{2} + \frac{x + 2}{3} + \frac{y + 3}{4} = \frac{4x + 3y}{12}$ /·12
6z + 6 + 4x + 8 +3y + 9 = 4x + 3y /-(4x + 3y + 23)
6z = -23 /:6
$z = -\frac{23}{6} = -3\frac{5}{6}$
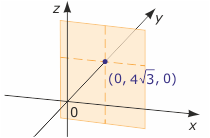Pierwiastkiem równania jest każda trójka liczb postaci (p, r, $-3\frac{5}{6}$), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, 0, $-3\frac{5}{6}$), (1, 7, $-3\frac{5}{6}$),
($\frac{1}{17}$, -4, $-3\frac{5}{6}$) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{( p, r,$-3\frac{5}{6}$) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę poziomą prostopadłą do osi OZ, przechodzącą przez punkt o współrzędnych (0, 0, $-3\frac{5}{6}$).
8) $\sqrt{3}y + \sqrt{5}z = -\sqrt{144} + \sqrt{\sqrt{3^2 + 4^2}}z$
Rozwiązanie
$\sqrt{3}y + \sqrt{5}z = -\sqrt{144} + \sqrt{\sqrt{3^2 + 4^2}}z$
prawa strona: wykonujemy pierwsze pierwiastkowanie i potęgowania pod pierwiastkami
$\sqrt{3}y + \sqrt{5}z = -12 + \sqrt{\sqrt{9 + 16}}z$
prawa strona: wykonujemy dodawanie pod pierwiastkami
$\sqrt{3}y + \sqrt{5}z = -12 + \sqrt{\sqrt{25}}z$
prawa strona: wykonujemy wewnętrzne pierwiastkowanie
$\sqrt{3}y + \sqrt{5}z = -12 + \sqrt{5}z$ /-$\sqrt{5}z$
$\sqrt{3}y= -12$ /:$\sqrt{3}$
$y = -\frac{12}{\sqrt{3}}$
prawa strona: usuwamy niewymierność z mianownika, mnożąc licznik i mianownik przez √3
y = - $\frac{12\sqrt{3}}{\sqrt{3}^2}$ = -4√3
Pierwiastkiem równania jest każda trójka liczb postaci (p, -4√3, r), gdzie p i r są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są trójki (0, -4√3, 0), (1, -4√3, -1),
(π, -4√3, -117) i inne. Rozwiązaniem równania są wszystkie takie trójki, czyli zbiór
{(p, -4√3, r) : p, r$\in$R}.
Tworzą one w przestrzeni płaszczyznę pionową prostopadłą do osi OY, przechodzącą przez punkt o współrzędnych (0, -4√3, 0).
rys. 22
9) 2(x+y+z) = 2x + 2y +2z
Rozwiązanie
Równanie to jest równoważne równaniu stopnia zero z trzema niewiadomymi 0 = 0. Jest to równanie tożsamościowe, którego pierwiastkiem jest każda trójka (p, q, r) liczb rzeczywistych, a rozwiązaniem jest zbiór wszystkich takich trójek, czyli R3 = {(p, q, r) : p, q, r$\in$ R}. Trójki te tworzą całą przestrzeń.
10) 2x + y - 5z = 2x + y - 5z +7
Rozwiązanie
Równanie to jest równoważne równaniu stopnia zero z trzema niewiadomymi 0 = 7. Jest to równanie sprzeczne, które nie ma pierwiastków, a jego rozwiązaniem jest zbiór pusty $\emptyset$.
A teraz spróbuj sam
1) Wskaż równania liniowe z trzema niewiadomymi. Dlaczego odrzuciłeś pozostałe?
- x0 + y1 + z2 + 1 = 0
- (x + y + z)1 = 22
- $\frac{x+y}{2} = \frac{x + z}{3} = \frac{1}{6}$
- $\frac{x+y}{2}-\frac{x + z}{3}=\frac{1}{6}$
- 5 = 0
- x - 2(y - 3(z - 4t)) = 5
- y1 - y2 + y3 - 17 = 1 - 2 + 3 - 17
- 17y1y2y3 = 17·1·2·3
- y + z1 - z2 = z2 + z1 - y
- $\frac{x_1 + y_1 - z_1}{\sqrt{2}} = \frac{x_2 - y_2 + z_2}{\sqrt{3}}$
2) Rozwiąż poniższe równania z trzema niewiadomymi i podaj ich pierwiastki
- z + x = 2y + x + 2
- 5x + 7y - 19z + 8 = 0
- 3z - 6(x - 2y) = 2(6y + z)
- $\frac{1}{5}(x - \frac{1}{7}(y - z + \frac{1}{9})) = \frac{1}{9}(z - \frac{1}{7}(y - x - \frac{1}{5}))$
- $\sqrt{2}z + (\sqrt{2} - 1)(x - y + 1) = \frac{z - y + x}{\sqrt{2} + 1}$
- 20z + (20 + 22)y - (21 + 25)x = 1z + 101y - 100010x
- $(\frac{\pi - 3,14}{\sqrt{2} - 1,41 + \sqrt{3} - 1,73} - 1)x = 0$
- $\frac{\sqrt{5} + 1}{2}z = \frac{2z}{\sqrt{5} - 1}$
- $\frac{1 + \sqrt{6}}{2}(1 + \frac{2}{5}(x + y - z)) = \frac{2}{\sqrt{6} - 1}(x + y - z + 1)$
Równania liniowe z n niewiadomymi zawierają n zmiennych, każdą w potędze co najwyżej jeden i co najmniej jeden współczynnik liczbowy przy tych zmiennych jest różny od zera.
Poza szczególnymi przypadkami równań tożsamościowych lub sprzecznych rozwiązania równań liniowych
- z 2 niewiadomymi stanowią jednowymiarową prostą na dwuwymiarowej płaszczyźnie,
- z 3 niewiadomymi stanowią dwuwymiarową płaszczyznę w trójwymiarowej przestrzeni.
Analogicznie rozwiązania równań liniowych
- z 4 niewiadomymi tworzą trójwymiarową przestrzeń w czterowymiarowej przestrzeni,
- z 5 niewiadomymi tworzą czterowymiarową przestrzeń w pięciowymiarowej przestrzeni,
- itd.
- z n niewiadomymi tworzą (n-1)-wymiarową przestrzeń w przestrzeni n-wymiarowej.
Rozwiązywanie równań z n niewiadomymi polega na tym, że wartości dla (n-1) zmiennych wybieramy dowolnie, a wartość n-tej zmiennej wyliczamy z podanego równania.
Przykłady
1) Rozwiąż równanie z czterema niewiadomymi
x4 = 2x1 + 8x2 - 7x3 + 1
Rozwiązanie
Pierwiastkiem równania jest każda czwórka liczb postaci (p1, p2, p3, 2p1 + 8p2 - 7p3 + 1 ), gdzie p1, p2 i p3 są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są czwórki (0, 0, 0, 1), (0, 0, 1/7, 0), (0, -1/8, 0, 0), (-1/2, 0, 0, 0), (1, 1, 1, 4) i inne. Rozwiązaniem równania są wszystkie takie czwórki, czyli zbiór
{ (p1, p2, p3, 2p1 + 8p2 - 7p3 + 1 ): p1, p2, p3 $\in$R}. Tworzą one trójwymiarową przestrzeń w przestrzeni czterowymiarowej przecinającą osie układu współrzędnych w punktach (0, 0, 0, 1), (0, 0, 1/7, 0), (0, -1/8, 0, 0), (-1/2, 0, 0, 0).
2) Rozwiąż równanie z pięcioma niewiadomymi
$2x_3-15x_5-\frac{1}{2}x_1=x_4- x_2$
Rozwiązanie
$2x_3-15x_5-\frac{1}{2}x_1=x_4-x_2$ /$-(2x_3-\frac{1}{2}x_1)$
$-15x_5=\frac{1}{2}x_1-x_2-2x_3+x_4$ /:(-15)
$x_5=-\frac{1}{30}x_1+\frac{1}{15}x_2+\frac{2}{15}x_3-\frac{1}{15}x_4$
Pierwiastkiem równania jest każda piątka liczb postaci (p1, p2, p3, p4, $-\frac{1}{30}p_1+\frac{1}{15}p_2+\frac{2}{15}p_3-\frac{1}{15}p_4$), gdzie p1, p2, p3 i p4 są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są piątki (0, 0, 0, 0, 0), (1, 0, 0, 0, $-\frac{1}{30}$), (0, 1, 0, 0, $\frac{1}{15}$), (0, 0, 1, 0, $\frac{2}{15}$ ), (0, 0, 0, 1, $-\frac{1}{15}$), (-30, 15, $\frac{15}{2}$, -15, 4) i inne. Rozwiązaniem równania są wszystkie takie czwórki, czyli zbiór
{(p1, p2, p3, p4, $-\frac{1}{30}p_1+\frac{1}{15}p_2+\frac{2}{15}p_3-\frac{1}{15}p_4$: p1, p2, p3, p4$\in$R}. Tworzą one czterowymiarową przestrzeń w przestrzeni pięciowymiarowej przechodzącą przez początek ukłądu współrzędnych (0, 0, 0, 0, 0).
3) Rozwiąż równanie z siedmioma niewiadomymi
$2x_3 + x_7 = \frac{51 + 6x_3}{3}$
Rozwiązanie
$2x_3 + x_7 = \frac{51 + 6x_3}{3}$ prawa strona: wykonujemy dzielenie
$2x_3 + x_7 = 17 + 2x_3$ /$-2x_3$
$x_7 = 17$
Pierwiastkiem równania jest każda siódemka liczb postaci (p1, p2, p3, p4, p5, p6, 17), gdzie p1, p2, p3, p4, p5, p6 są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są siódemki (0, 0, 0, 0, 0, 0, 17), (1, 0, 0, 0, 0, 0, 17), (0, -5, 0, 0, 0, 0, 17), (0, 0, 33, 0, 1/2, 0, 17), i inne. Rozwiązaniem równania są wszystkie takie siódemki, czyli zbiór {(p1, p2, p3, p4, p5, p6, 17) : p1, p2, p3, p4, p5, p6$\in$R}. Tworzą one przestrzeń sześciowymiarową w przestrzeni siedmiowymiarowej ortogonalną ("prostopadłą") do osi OX7, przechodzącą przez punkt o współrzędnych (0, 0, 0, 0, 0, 0, 17).
4) Rozwiąż równanie z dziesięcioma niewiadomymi
$-3x_1+2(x_2+x_3+...+x_{10})+12=\frac{3x_{10}-2x_1}{6}$
Rozwiązanie
$-3x_1 + 2(x_2 + x_3 + ... + x_{10}) + 12 = \frac{3x_{10} - 2x_1}{6}$ prawa strona: wykonujemy dzielenie
$-3x_1 + 2(x_2 + x_3 + ... + x_{10}) + 12 = 2x_{10} - 3x_1$ /$-(2x_{10} + 2x_9 - 3x_1)$
$2(x_2 + x_3 + ... + x_8) + 12 = -2x_9$ /:(-2)
$(-1)(x_2 + x_3 + ... + x_8) + 12 = x_9$ lewa strona: wykonujemy mnożenie
$-x_2-x_3-...-x_8+12=x_9$
Pierwiastkiem równania jest każda dziesiątka liczb postaci (p1, p2, ..., p8, $-p_2-p_3-...-p_8+12$, p9), gdzie p1, p2, ..., p9 są dowolnymi liczbami rzeczywistymi, np. pierwiastkami tego równania są dziesiątki (0, 0, ..., 0, 12, 0), (1, 1, ..., 1, 5, 1), (-123, 0, 12, $-\frac{1}{2}$, -18, 2, 3, 9, $-7\frac{1}{2}$, $\pi$) i inne. Rozwiązaniem równania są wszystkie takie dziesiątki, czyli zbiór
{(p1, p2, ..., p8, $-p_2-p_3-...-p_8+12$, p9) : p1, p2, ..., p9$\in$R}. Tworzą one dziewięciowymiarową przestrzeń w przestrzeni dziesięciowymiarowej, która nie ma punktów wspólnych z osiami OX1 i OX10.
5) Rozwiąż równanie z siedemnastoma niewiadomymi
$x_1+2x_2+...+17x_{17}=x_{17}+(x_{17}+x_{16})+...+(x_{17}+x_{16}+...+x_1)$
Rozwiązanie
Równanie to jest równoważne równaniu stopnia zero z siedemnstoma niewiadomymi 0 = 0. Jest to równanie tożsamościowe, którego pierwiastkiem jest każda siedemnastka (p1, p2, ..., p17) liczb rzeczywistych, a rozwiązaniem jest zbiór wszystkich takich siedemnastek, czyli R17 = {(p1, p2, ..., p17) : p1, p2, ..., p17$\in$ R}. Siedemnastki te tworzą całą przestrzeń siedemnastowymiarową.
6) Rozwiąż równanie ze stoma niewiadomymi
$1-x_{100}+x_{79}=-(x_{100}- x_{79})$
Rozwiązanie
Równanie to jest równoważne równaniu stopnia zero ze stoma niewiadomymi 1 = 0. Jest to równanie sprzeczne, które nie ma pierwiastków, a jego rozwiązaniem jest zbiór pusty $\emptyset$.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
